6.2 The key Deliverables of Constructional Architecture
For any system S, constructional architecture has five core types of deliverables:
- the constructional requirement architecture diagram that hierarchically organizes all constructional requirements – with respect to S – according to an refinement hierarchy,
- the constructional mode diagram that describes how S passes – with indication of the associated events – from a configuration to another one, starting from its birth up to its death,
- the constructional decomposition & interaction diagrams that are describing – in a purely static way – the components of S with their interactions1 Usually only at global level, but also possibly in only a given configuration,
- the constructional scenario diagrams that are describing – in a dynamic way – the interactions taking place between the components of S, in a given functional mode,
- the constructional flow diagrams that synthetizes all flows – with their logical relationships – absorbed or produced by the components of S during the “configuration cycle”2That is to say the period of time modeled by the configuration diagram. of S.
These different types of deliverables are presented more in details below.
6.2.1 Constructional Requirement Architecture Diagram
Let S be a system. The constructional requirement architecture diagram of S is then a hierarchical exhaustive representation of all constructional requirements of S, a constructional requirement R1 being under another constructional requirement R2 in this hierarchy if and only if one can logically deduce R1 from R23Remember that constructional requirements are logical predicates (see subsection 2.4.3). In this last situation, one says then more precisely that R2 refines into R1, which explains why one speaks of a constructional requirement refinement hierarchy.
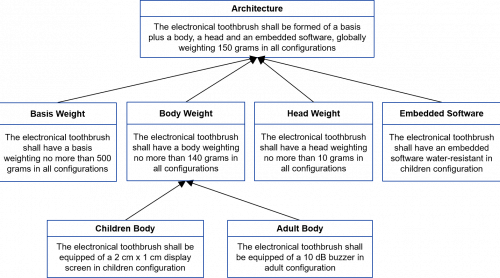
Figure 54 – Example of a constructional requirement architecture diagram for an electronical toothbrush
The above Figure 54 shows a (quite partial) constructional requirement architecture diagram for an electronic toothbrush, a constructional requirement being – classically and similarly both to a need and to a functional requirement – represented here by a 2-part box, whose first top part is a short name summarizing the constructional requirement scope and second bottom part is dedicated to the constructional requirement statement, when the different refinement relationships on which relies the constructional requirement hierarchy are – also classically – represented by arrows.
The same issue that was already pointed out, both for need and functional requirement architecture diagrams, also happens in the same terms for the constructional requirement architecture diagram: organizing a constructional requirement refinement hierarchy is indeed always difficult since one shall avoid to have too much constructional requirements of first level, but of course also too many levels of refinements, as soon as one wants to be able to efficiently use such a view. The 7x7x7 rule (see first part of subsection 3.2) is again precious to handle this real difficulty. As a consequence, a typical “good” constructional requirement architecture diagram associated with a given system shall have no more than 7 high level constructional requirements, each of them being refined in around 7 medium level constructional requirements, finally also refining in the same way into 7 low level constructional requirements. Note again that the number 7 is just an order of magnitude. Obtaining up to 10-12 high level constructional requirements in a constructional requirement architecture diagram could of course work: however one must probably not go further without analyzing whether this number is justified. Finally one shall not hesitate to construct as many additional constructional requirement architecture diagrams as necessary, for refining such an analysis as soon as all relevant constructional requirements are not derived and/or captured.
6.2.2 Configuration Diagram
Let S be again a system. The configuration diagram of S is then a representation of:
- the configurations of S, with their relative temporal relationships (consecutiveness, inclusion or simultaneity)4 We refer to the second paragraph of subsection 4.2 in this matter,
- the events that cause the different transitions between each configuration of S and the immediately consecutive ones.
The standard representations of the temporal relations between configurations introduced above are given – mutatis mutandis – by Table 10, if one now interprets there C and D as configurations.
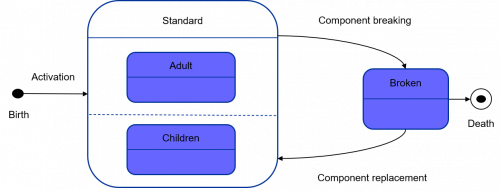
Figure 55 – Example of configuration diagram for an electronical toothbrush
The above Figure 55 provides an example of configuration diagram associated with an electronical toothbrush, which is here quite simple, taking the standard representation of configurations and of their temporal relationships that we introduced, when events – that induce configuration transitions – are modeled by arrows labelled with the name of the relevant event. Note also that the initial (resp. termination) events in each configuration do not respect this rule since they are just conventionally modeled by small black circles (resp. by white circles containing a black circle).
The configuration diagram is key since it models – from a purely constructional perspective – time, even if it is not immediately obvious to see here. Following the intuition that we developed at the end of the second paragraphs of sections 4.2 and 5.2, one could consider that the next diagrams – i.e. the constructional decomposition & interaction diagrams – are modeling the “constructional space” in which components are evolving. Since space and time are always both required to specify any constructional reality (that takes place somewhere at a certain time), one can easily see that these two diagrams are completely complementary.
6.2.3 Constructional Decomposition & Interaction Diagram
Let S be a system. The constructional decomposition diagram associated with S is then a hierarchical representation of the components of S, a set C1, C2, …, CN of components being under another component D in this hierarchy if D is the result of the integration – in the meaning of Definition 0.5 – of the components C1, …, CN5 Due to our definition of the integration operator, this hierarchy is therefore again an abstraction hierarchy. (C1, …., CN are then classically called “sub-components” of D). The constructional interaction diagrams associated with S are then just the different representations – there is one constructional interaction diagram per integration relation involved in the constructional decomposition diagram – of each such integration relationship that does exist between the different components appearing in the hierarchy modeled by the constructional decomposition diagram.
The following Figure 56 now provides an illustrative partial example of constructional decomposition diagram for an electronic toothbrush, where the integration relationships on which such an hierarchy relies are – quite classically – represented by black-squared (resp. white-squared) arrows when the low-level component is mandatory (resp. optional – which allows to model product options using this last syntax – ) with respect to the depicted integration relationship.
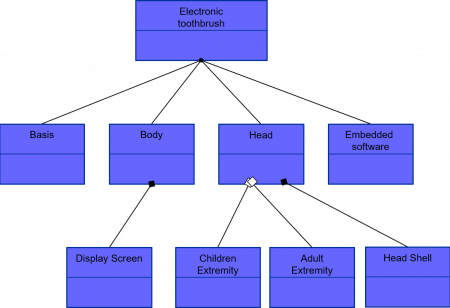
Figure 56 – Example of a constructional decomposition diagram for an electronical toothbrush
We also give an example of a constructional interaction diagram for an electronical toothbrush that can be found in Figure 57. It provides the integration relationship existing between the electronic toothbrush in its whole and its first “sub-components” as they are appearing above in the previous constructional decomposition diagram.
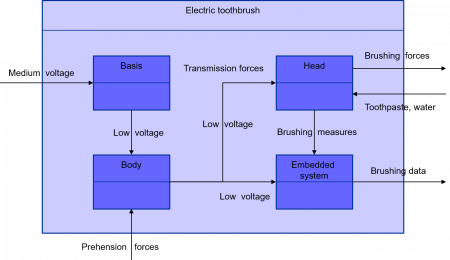
Figure 57 – Example of a constructional interaction diagram for an electronical toothbrush
The constructional decomposition of a system S modeled by the constructional decomposition diagram is also classically called the Product Breakdown Structure (PBS) of S. Similarly to the Mission or the Functional Breakdown Structures that we introduced in the two last chapters, it provides the exhaustive dictionary of components of the system and has a key role in guaranteeing a common understanding on the constructional scope of a system, which is mandatory for efficient transversal collaboration between the different actors and stakeholders of a system development project.
One must however beware to the good readability of such a view. Just observe in this matter that all the recommendations based on the 7x7x7 rule that we previously gave for the stakeholder and the need architecture diagrams of course also apply – mutatis mutandis – for efficiently modeling the Product Breakdown Structure of a given system.
Note also that Figure 9 in Chapter 0, even if formally functionally oriented, can also be easily reinterpreted as a constructional interaction diagram, here associated with an aircraft: each “box” of this diagram, even if, strictly speaking, representing a first-level sub-function of an aircraft, may indeed also naturally be interpreted as a first-level sub-system of an aircraft.
6.2.4 Constructional Scenario Diagram
Let again S be a system and q(S) a configuration of S. A constructional scenario diagram associated with S and q(S) is then a dynamic representation of the interactions that are taking place between the components of S during the period of time which is modeled by q(S).
The following Figure 58 shows an example of constructional scenario diagram, associated with the “Children” configuration of an electrical toothbrush. It shows how the electronic toothbrush sends an encouraging message to the end-user when in a children configuration (see subsection 2.4.3 for the corresponding illustration). We do refer to the suitable paragraph of subsection 2.4.2 for all the details on the semantics of the below representation.
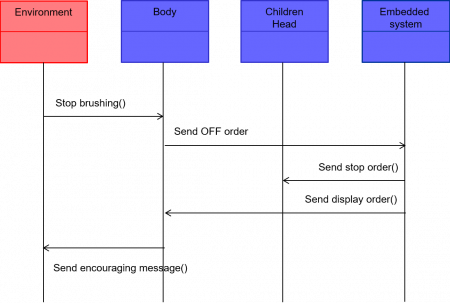
Figure 58 – Example of a constructional scenario diagram for an electronical toothbrush
A constructional scenario diagram provides therefore the explicit “algorithm” which is underlying to the constructional interactions of the system that occur in a given configuration. This is key to finely understand what concretely happens during a given configuration. Observe finally that this last diagram has also a functional nature since it models in a certain way a “constructional behavior”: one shall thus always beware not to overlap at this level with functional architecture in order to avoid to make two times similar analyses.
6.2.5 Constructional Flow Diagram
Let S be a system. The constructional flow diagram associated with S is a consolidated description of all constructional flows associated with S and of respectively:
- their logical relationships,
- their abstraction relationships (see the last paragraph of Chapter 4).
Hence it plays the role of the constructional “data model”6Beware that, even if we use the syntax of a data model for the constructional flow diagram, this last diagram is again not really a data model since it does not represent (only) data, but also physical objects, business objects or even informal information that may be exchanged with “humanware” stakeholders of a given system. of the system. Note that one also may split this diagram into two diagrams, each of them covering the two above points.
The Figure 59 that follows shows an example of (partial) constructional flow diagram, associated with an electrical toothbrush. It can be constructed by consolidating all the constructional flows that are appearing in the high-level constructional interaction diagram which is provided by Figure 57 for an electronical toothbrush. Its syntax follows exactly the same principles than for the operational & functional flow diagrams (see the last paragraph of the last two previous chapters).
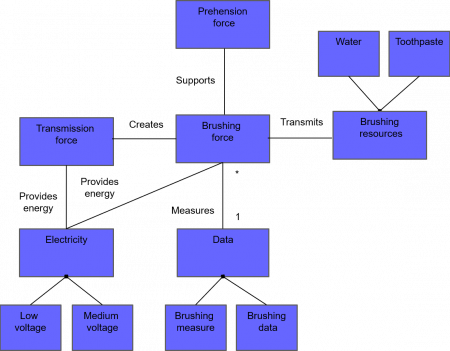
Figure 59 – Example of constructional flow diagram for an electronical toothbrush
As already stated, such a constructional flow diagram defines the constructional flow or object model of a given system. It is therefore completely “dual” to the constructional decomposition, interaction or scenario diagrams since it focuses only on flows and absolutely not on the different components of the system that are producing these flows.
We must therefore emphasize that such a diagram is of high importance since it rationally describes in a consolidated and organized way all inputs and all outputs of the components of a given system. Hence it gives the constructional “dictionary” of the system, that is to say the list of all objects that are constructionally – that is to say concretely – manipulated by the system. Hence this dictionary is of high value for ensuring a common vision between all project actors involved in the architecting process: these actors shall normally – in an ideal world – only use the terms of that dictionary when discussing of a constructional object. One may easily understand that such a principle allows to avoid any ambiguity between the different project actors. It is thus completely key for ensuring a good collaboration between these actors.