0.1 CESAM: a Mathematically Sound System Modeling Framework

0.1 CESAM: a Mathematically Sound System Modeling Framework

CESAMES Systems Architecting Method (CESAM) is the result of 12 years of research & development (cf. [1], [3], [4], [16], [17], [18], [22], [27], [48], [49], [51], [52], [53]) including permanent interactions and operational experimentations with industry. The CESAM framework was indeed used in practice within several leading international industries in many independent areas with a success that has never wavered (see [14], [23], [26], [31], [32], [33], [35] or [36]) for some application examples). This huge theoretical and experimental effort resulted in a both mathematically sound & practical system modeling framework, easy to use by working systems engineers and architects.
We shall only present in this general introduction the more important fundamentals¹CESAM framework is based on formal semantics, the mathematical theory – based on mathematical logics (cf. [12]) – which provides the fundamentals of computer science (see [89]) CESAM framework may be understood as an extension of usual formal semantics – which only addresses software systems – to more general types of systems. of the CESAM framework that may help to better understand its philosophy. At this level, the key point is the logical consistency of the CESAM framework, naturally provided by its mathematical basis. Due to this strong consistency, anybody who agrees with logical reasoning²Logical reasoning is usually mixed with common sense. However one shall not forget that logics is a body of mathematical knowledge (see [12]), sadly largely unknown to engineers, that can be traced back to Aristoteles (see [84]). (which shall normally be the case with all engineers) will indeed be able to use and work with CESAM framework.

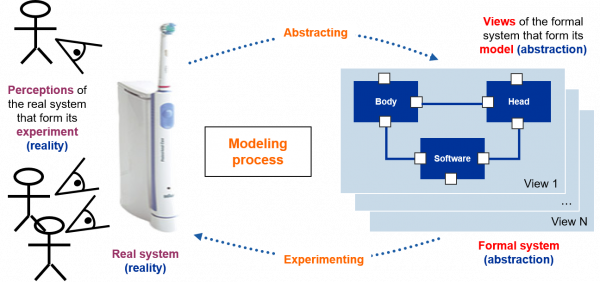
Figure 1 – The two abstracting/ experimenting sides of a system modeling process

Note now first that systems are considered in a modelling perspective within CESAM framework. This point of view immediately leads to distinguish the two core concepts of “formal system” and “real system”. It is indeed quite important to avoid making any confusion³Unfortunately this confusion is quite common in systems engineering where such a distinction is usually not made both in practice and in most textbooks, handbooks and standards (such as [15], [42], [44], [47], [57], [61], [62], [71], [74] or [78]). Aslaksen appears in particular to be one of the rare systems engineering authors who proposed a formal definition for a system (see [9] or [10]). Sound systems modelling formalisms thus seem to be only found in the mathematical simulation literature (cf. [23], [73] or [100]) or in the few theoretical computer science system literature (cf. [21], [55] or [59]). between the result of a system modelling process (the formal system) and the concrete object under modelling (the real system). Many design mistakes – with often high costs of non-quality – are indeed made by engineers when they forget that their system specification documentation is just an abstraction of reality, but not the “real” reality, and that their job is to ensure permanent alignment – through feedback loops with reality – between their system models and the real system, as it is and not as they think it is.

A system modeling process can thus be seen as a permanent back-and-forth between, on a first side, an abstraction activity that constructs a formal model of a real world object – using the tools of systemic analysis – and on a second side, an experimentation activity where the structure or behavior of the real object, as given or predicted by the model, are checked against those really observed in reality. The real object under modelling will thus be considered as a (real) system due to the fact that a system modeling process analyzes it as a (formal) system within a systemic modelling framework. By abuse of language, we often identify these two concepts of “system”, but it is important never to forget that “the map is not the territory” ([46]) in order to know at any time on what we reason! Note also that this approach points out that being a system is absolutely not an intrinsic property of an object⁴This last consideration shows that it is merely impossible to give a sound definition of a real system since any object in the real world can be considered as a system as soon as a system designer decides it. , but results from a modelling decision of a system designer. This being recalled, we can now provide the definition of a formal system⁵The CESAM definition of a system provided by Definition 0.1 unifies two classical system modelling traditions: it indeed mixes the usual functional definition coming from the mathematical system simulation literature (cf. [23], [73] or [100]) and the state-machine system definition that emerged in theoretical computer science (cf. [21], [55] or [59]). on which relies the CESAM modelling framework.

Definition 0.1 – Formal system– A formal system S is characterized on one hand by a input set X, an output set Y and an internal variables set Q and on the other hand by the following two kinds of behaviors that link these systemic variables among a given time scale T⁶A time scale T is a totally ordered set with a unique minimal element – usually denoted t₀ – and where each element t ∈ T has a (unique) greatest upper bound within the time scale, called its successor and denoted t+ within T. Up to rescaling, two types of time scales are key in practice: discrete time scales where t+ = t + 1 and continuous time scales where t+ = t + dt where dt stands for an infinitesimal quantity. Discrete time scales model event-oriented systems (such as software systems which are regulated by a discrete clock) when continuous time scales are used to model physical continuous phenomena. :

• a functional behavior that produces an output y(t+) ∈ Y at each moment of time t ∈ T, depending on the current input x(t) ∈ X and internal state q(t) ∈ Q of the system ;
• an internal behavior that results in the evolution q(t+) ∈ Q of the internal state at each moment of time t ∈ T, under the action⁷When this action is not permanent, one may identify the involved input to a discrete event which occurs only at a certain moment of time t ∈ T, considered as instantaneous within T. Note however that an event is always relative to a given time scale: it may indeed not be instantaneous when analyzed from another, more refined, time scale. of a system input x(t) ∈ X.

Figure 2 – Standard representation of a formal system

This definition is deliberately very weak following Occam’s razor strategy⁸Occam’s razor (see [84]) is a key scientific parsimony principle which expresses that there is no need to introduce a new
concept when it can be explained by already existing concepts. The CESAM system modeling framework is constructed in that way: we always only introduced the minimal number of new architectural concepts that are necessary for system modelling purposes. This typically explains why we proposed such a simple system definition: it is indeed minimal for understanding the structure of CESAM framework (see end of section 0.1). that prevails throughout CESAM framework. It simply means that a system is just defined by an input/output and an internal behavior⁹The internal behaviour of a system is modelled by an evolution law of its internal variables, called “states”.. This is of course not abnormal since we do want to capture commonalities between ALL real systems. These common points are therefore mechanically quite limited due to the tremendous diversity of the real objects to take into account. However we now have a unified system modelling framework, provided by the below Definition 0.2, in which we can uniformly reason on any type of systems and hence think system integration, which was one of our first goals (see section 0.2)

Definition 0.2 – Real system – An object of the real world will be called a real system as soon as its structure and its behavior can be described by a formal system (in the meaning of Definition 0.1) that will be then called a model of the considered real system.

According to this definition, quite all human artefacts – independently of their physical, informational or organizational nature – can thus be considered and analyzed as systems. Only changes the nature of the laws – given by physics, logics or sociology – that allow defining the functional and internal behaviors which are making them systems. The two previous definitions also help to understand that it is neither the nature, nor the size, nor the hierarchical position¹⁰A common mistake is for instance to consider that a “sub-system” of a system (see next section 0.2 for more details) is not a system, which is of course absolutely not the case according to our definitions (this remark allows in particular to apply recursively the principles of system modelling within a given system hierarchy). that makes something a system, since quite all real objects can be seen as systems. As already pointed out, considering that an object is a system remains first of all a modelling (human) choice: it just means that this object will be abstracted through a systemic point of view, i.e. in the framework given by Definition 0.1.

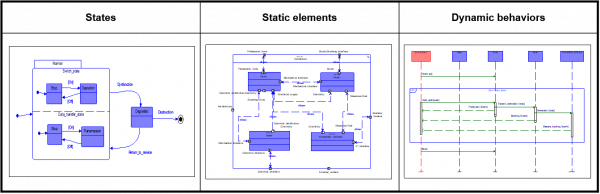
Figure 3 – Structure of a standard complete system specification

Note finally that the definitions we proposed above imply that a system S is completely specified (for a given time scale) if and only one is able to provide (see Figure 3):

1. the states of S, i.e. a description of the evolution law of its internal variables, which can be typically achieved through a state-machine (see for instance [20] or [21]),
2. a description of its functional dynamics, which can be naturally obtained through defining:
   o the static elements of S, in other terms the signatures of the functions required to express its functional behavior, which can be given by a static block-diagram (see [34] or [73]),
   o the dynamic behavior of S, that is to say the temporal dynamics¹¹We here mean the underlying “algorithm” that expresses how the functional behaviour of S is obtained as a result of the
   interactions of a certain number of functions. of these functions, which can be for instance defined by a sequence diagram (see [20] or [34]).

These last considerations are at the core of the CESAM systems architecting matrix (see section 2.5) and do explain the generic nature of the key columns (states, static elements, dynamic behaviors as described in Figure 3) involved in that modelling matrix.
Note that it may be useful to consolidate in a specific view all the exchanged input/output flows that do appear when describing the functional dynamics of a system. Such a view – which strictly speaking is already contained in the two other functional views introduced above – is indeed important for constructing the glossary of all flows exchanged within a system. This will lead us to the last column (objects) of the CESAM systems architecting matrix (see section 2.5).
Up to now, we however only dealt with an extensional formalism for systems. When using Definition 0.1, we are indeed obliged by construction to explicitly describe extensionally the behavioral and structural dimensions of a system (definition in extension). But there exists another different, but totally equivalent from a mathematical perspective, system specification formalism which is of intentional nature. This means that we do not need here to describe the behavior or structure of a system as before, but rather to express its expected/intended properties (definition in intension).
That new formalism is based on a formal logic, called system temporal logic, which is presented in full details in Appendix A. The only point to stress here is that we will now need to work with systems whose input, output and internal states sets X, Y, Q and timescale T are fixed. The associated system temporal logic allows then to syntactically define well-formed logical formulae¹²Also called predicates in formal logic. , called temporal formulae, which specify the sequences O of inputs, outputs and internal states values of such a system that can be observed among all moments of time t within the timescale T, as stated below:

O = (O(t)) for all t ∈ T, where we set O(t) = (x(t), y(t), q(t))¹³We use here the formalism of Definition 0.1

We are now in position to introduce the notion of formal system requirement which refers to logical predicates within system temporal logic (see Appendix A for several examples).

Definition 0.3 – Formal requirement – Let S be a formal system with X, Y and Q as input, output and internal states sets and T as timescale. A formal requirement on S is a temporal formula expressed in system temporal logic, based on X, Y, Q, and T as described in Appendix A.
Most of engineers would however be afraid working with system temporal logic. One is hence quite rarely¹⁴Temporal logic is only classically used for the verification of real-time critical software systems. using formal requirements to specify real systems. The only utility of the previous definition will then just be to remember that one works with logical formalisms when one manages systems requirements, which is usually forgotten. This explains why we now propose the following unformal definition that intends to reflect what should be a good requirements engineering practice¹⁵A good system requirement shall indeed always be unambiguous which will never be achieved when trying to express a formal requirement in natural language..

Definition 0.4 – Requirement – A requirement on a real system S is then any sentence that intends to express a formal requirement on a formal system that models S.
Note that each formal requirement R specifies a set of systems, which is the set of all formal systems that satisfy to R. A set SR of formal requirements specifies then also a set of formal systems, that is to say the set of formal systems that satisfy to all elementary requirements of SR. This simple property does establish a connection between sets of (formal) requirements and sets of (formal) systems. One can then prove that this connection is bijective, which means in other terms that it is mathematically strictly equivalent to specify sets of systems using either Definition 0.1 or sets of requirements. We thus have introduced two different equivalent ways of specifying systems.

A wrong conclusion would now be to use either one, or the other formalism, for defining systems. Our two formalisms are indeed absolutely not equivalent in terms of engineering effort: some properties are indeed much easier to state using the formalism of Definition 0.1 when some others are much simpler to state using requirements¹⁶The fact that a system behaves according to a given state machine is for instance easier to state by explicitly describing the concerned state machine, which gives rise to a single systemic view. Using requirements would contrarily require to define one logical formula per transition – stating typically that when the system is in state q and event e occurs, it shall pass in state q’ – which would give rise to N requirements where N is the number of involved transitions, which is clearly much more complicated than the first formalism. Conversely a safety property can usually be stated using just one unique requirement, but would give rise to many behavioral descriptions if one would like to express it in that other way. . The working systems engineer will thus always have to mix extensional and intentional formalisms, according to their relative “human” costs. A good system specification is therefore a specification that shall mix on one hand behavioral or structural descriptions in the line of Definition 0.1 and Definition 0.2 and on the other hand requirements in the line of Definition 0.3 and Definition 0.4.

Note finally that requirements will also provide us the first column (expected features) of the CESAM systems architecting matrix (see section 2.5)¹⁷As a matter of fact, the systems architecture paradigm can also be expressed using the formalism of requirements. Any systems architecture problem can indeed be stated as the research of a system S that satisfy a set of requirements associated with the environment of S. As an immediate consequence of this genericity, the generic structure of a system provided by CESAM framework naturally reflects in the generic structure of the systems architecture process, which is the core property on which the CESAM systems architecting method relies..

Table of contents

References

[1] Abts C., Boehm B., Brown W. A., Chulani S, Clark B.K., Horowitz E., Madachy R., Reifer D.J., Steece B., Software Cost Estimation with COCOMO II (with CD-ROM), Englewood Cliffs, Prentice-Hall, 2000

[3] Aiguier M., Golden B., Krob D., Modeling of Complex Systems II : A minimalist and unified semantics for heterogeneous integrated systems, Applied Mathematics and Computation, 218, (16), 8039-8055, doi : 10.1016/j.amc.2012.01.048, 2012

[4] Aiguier M., Golden B., Krob D., An adequate logic for heterogeneous systems, [dans Proceedings of the 18th International Conference on Engineering of Complex Computer Systems (ICECCS’ 2013), Y. Liu, A. Martin, Eds.], IEEE, 2013

[14] Berrebi J., Krob D., How to use systems architecture to specify the operational perimeter of an innovative product line ?, [dans “Proceedings of INCOSE International Symposium of 2012 (IS 2012)”, M. Celentano, Ed.], 15 pages, INCOSE, 2012

[16] Bliudze S., Krob D., Towards a Functional Formalism for Modelling Complex Industrial Systems, [dans “European Conference on Complex Systems’’ (ECCS’05), P. Bourgine, F. Képès, M. Schoenauer, Eds.], (article 193), 20 pages, 2005

[17] Bliudze S., Krob D., Towards a Functional Formalism for Modelling Complex Industrial Systems, ComPlexUs, Special Issue : Complex Systems – European Conference – November 2005 – Selected Papers – Part 1, 2, (3-4), 163-176, 2006

[18] Bliudze S., Krob D., Modeling of Complex Systems – Systems as data-flow machines, Fundamenta Informaticae, Special Issue : Machines, Computations and Universality, 91, 1-24, 2009

[20] Booch G., Jacobson I., Rumbaugh J., The Unified Modeling Language Reference Manual, Second Edition, Addison-Wesley, 2004

[21] Börger E., Stärk R., Abstract state machines, Springer, 2003

[22] Caseau Y., Krob D., Peyronnet S., Complexité des systèmes d’information : une famille de mesures de la complexité scalaire d’un schéma d’architecture, Génie Logiciel, 82, 23-30, 2007

[23] Cha P.D., Rosenberg J., Dym C.L., Fundamentals of modeling and analyzing engineering systems, Cambridge University Press, 2000

[26] Dauron A., Douffène A. , Krob D., Complex systems operational analysis – A case study for electric vehicles, [dans Posters of the 2nd international conference on “Complex Systems Design & Management” (CSDM 2011), O. Hammami, D. Krob, J.L. Voirin, Eds.], 18 pages, 2011

[27] de Neufville R., The Baggage System at Denver: Prospects and Lessons, Journal of Air Transport Management, Vol. 1, No. 4, Dec., 229-236, 1994

[31] Doufène A., Krob D., Sharing the Total Cost of Ownership of Electric Vehicles : A Study on the Application of Game Theory, [dans Proceedings of INCOSE International Symposium of 2013 (IS2013)], 2013

[32] Doufène A., Krob D., Model-Based operational analysis for complex systems – A case study for electric vehicles, [dans Proceedings of INCOSE International Symposium of 2014 (IS2014)], 2014

[33] Doufène A., Krob D., Pareto Optimality and Nash Equilibrium for Building Stable Systems, IEEE International Systems Conference, 2015

[34] Friedenthal S., Moore A.C., Steiner R., A Practical Guide to SysML : the Systems Modeling Language, Morgan Kaufmann OMG Press, 2012

[35] Giakoumakis V., Krob D., Liberti L., Roda F., Optimal technological architecture evolutions of Information Systems, [dans Proceedings of the first international conference on “Complex Systems Design & Management” (CSDM 2010), M. Aiguier, F. Bretaudeau, D. Krob, Eds.], 137- 148, Springer Verlag, 2010

[36] Giakoumakis V., Krob D., Liberti L., Roda F., Technological architecture evolutions of Information Systems : trade-off and optimization, Concurrent Engineering : Research and Applications, Volume 20, Issue 2, 127-147, 2012

[48] Krob D., Modelling of Complex Software Systems : a Reasoned Overview, [dans “26th IFIP WG 6.1 International Conference on Formal Methods for Networked and Distributed Systems” (FORTE’2006), E. Najm, J.-F. Pradat-Peyre, V. Viguié Donzeau-Gouge, Eds.], Lecture Notes in Computer Science, 4229, 1-22, Springer Verlag, 2006 (Invited speaker)

[49] Krob D., Architecture of complex systems : why, what and how ?, [dans Proceedings of “COgnitive systems with Interactive Sensors (COGIS’07)”, H. Aghajan, J.P. Lecadre, R. Reynaud, Eds.], Stanford University, 1 page, 2007 (Invited speaker)

[51] Krob D., Eléments d’architecture des systèmes complexes, [in “Gestion de la complexité et de l’information dans les grands systèmes critiques”, A. Appriou, Ed.], 179-207, CNRS Editions, 2009

[52] Krob D., Eléments de systémique – Architecture de systèmes, [in Complexité-Simplexité, A. Berthoz – J.L. Petit, Eds.], Editions Odile Jacob, 2012

[53] Krob D., Eléments de modélisation systémique, [in L’Energie à découvert, R. Mossery – C. Jeandel, Eds.], CNRS Editions, 2013

[73] Severance F.L., System modeling and simulation – An introduction, Wiley, 2001

Our social networks